El Lado Oculto de los Irracionales

lunes, 20 de enero de 2014

INVESTIGACION DE NÚMEROS IRRACIONALES PI e Y PHI

MATEMÁTICAS IV

Maria Margarita Sanchez Flores
Números irrracionales pi, e y phi

Miembros de la CANACA:

Fundador:
Torres Escalona Andrés
Cofundadores:
Lázaro Perez Juan Carlos
Medina Ortiz Hugo Fernando
Velazquez Benito Gilberto

GRUPO 404

ESCUELA NACIONAL PREPARATORIA 1 "GABINO BARREDA"
_______________________________________________________________________________

OBJETIVO:

Nuestro objetivo de este trabajo es sacar una buena calificacion en el 2do periodo ademas de tener el mejor blog de los irracionales de nuestra clase.
_________________________________________________________________________________

CONCLUSIÓN:
Aprendimos mas sobre la utilidad e importancia de estos números ademas de sus aplicaciones en la vida, tambien aprendimos algo sobre cálculo y la historia de los grandes matemáticos y las matemáticas mismas.

________________________________________________________________________________

REFERENCIAS:
http://es.wikipedia.org/wiki/N%C3%BAmero_e
http://es.wikipedia.org/wiki/N%C3%BAmero_%C3%A1ureo
http://es.wikipedia.org/wiki/N%C3%BAmero_%CF%80

Libro del CONAMAT del 2010.
_________________________________________________________________________________

INTRODUCCION A LOS NÚMEROS IRRACIONALES

Primero hay que definir a los racionales.

Un racional es cumple con:

En cuanto, un irracional es simplemente:

Entonces decimos, un número irracional es un número que no puede ser expresado como una fracción $\frac{m}{n}$ , donde $m$ y $n$ son enteros y $n$ es diferente de cero. Es cualquier número real que no es racional.

Tras distinguir los números componentes de la recta real en tres categorías: (naturales, enteros y racionales), podría parecer que ha terminado la clasificación de los números, pero aun quedan "huecos" por rellenar en la recta de los números reales. Los números irracionales son los elementos de dicha recta que cubren los vacíos que dejan los números racionales.

Los números irracionales son los elementos de la recta real que no pueden expresarse mediante el cociente de dos enteros y se caracterizan por poseer infinitas cifras decimales no periódicas. De este modo, puede definirse al número irracional como un decimal infinito no periódico. En general, toda expresión en números decimales es solo una aproximación en números racionales al número irracional referido, por ejemplo, el número racional 1,4142135 es solo una aproximación a 7 cifras decimales del número irracional raíz cuadrada de 2, el cual posee infinitas cifras decimales no periódicas.

Entonces, decimos con toda propiedad que el número raíz cuadrada de dos es aproximadamente igual a 1,4142135 en 7 decimales, o bien es igual a 1,4142135… donde los tres puntos hacen referencia a los infinitos decimales que hacen falta y que jamás terminaríamos de escribir.

Debido a ello, los números irracionales más conocidos son identificados mediante símbolos especiales; los tres principales son los siguientes:

$\pi$ (Número "pi" 3,14159 ...): razón entre la longitud de una circunferencia y su diámetro.
e (Número "e" 2,7182 ...): $\lim _{n \to +\infty} \left( 1 + \frac {1}{n}\right) ^{n}$
$\Phi$ (Número "áureo" 1,6180 ...): $\frac{1 + \sqrt{5}}{2}$

-e- de Euler

La constante matemática $e\,$ es uno de los más importantes números reales. Se relaciona con muchos interesantes resultados. Por ejemplo, la derivada de la función exponencial $f(x)=e^x\,$ es esa misma función. El logaritmo en base $e\,$ se llama logaritmo natural o neperiano.

El número $e\,$ , conocido a veces como número de Euler, fue reconocido y utilizado por primera vez por el matemático escocés John Napier, quien introdujo el concepto de logaritmo en el cálculo matemático.

Es considerado el número por excelencia del cálculo, así como $\pi\,$ lo es de la geometría y el número $i\,$ del análisis complejo. El simple hecho de que la función $e^x\,$ coincida con su derivada hace que la función exponencial se encuentre frecuentemente en el resultado de ecuaciones diferenciales sencillas. Como consecuencia de esto, describe el comportamiento de acontecimientos físicos regidos por leyes sencillas, como pueden ser la velocidad de vaciado de un depósito de agua, el giro de una veleta frente a una ráfaga de viento, el movimiento del sistema de amortiguación de un automóvil o el cimbreo de un edificio metálico en caso de terremoto. De la misma manera, aparece en muchos otros campos de la ciencia y la técnica, describiendo fenómenos eléctricos y electrónicos (descarga de un condensador, amplificación de corrientes en transistores BJT, etc.), biológicos (crecimiento de células, etc.), químicos (concentración de iones, periodos de semidesintegración, etc.), y muchos más.

El número $e\,$ , al igual que el número $\pi\,$ y el número áureo (φ), es un irracional, no expresable por la razón de dos enteros; o bien, no puede ser expresado con un número finito de cifras decimales o con decimales periódicos. Además, es un número trascendente, es decir, que no puede ser obtenido mediante la resolución de una ecuación algebraica con coeficientes racionales.

Aplicaciones:

Decaimiento radiactivo, incremento de poblaciones, Ley de enfriamiento de Newton, Cálculo, modelos de la vida, enteros continuos, probabilidad y estadística, etc etc etc.

Videos de lo que aportó Leonhard Paul Euler

https://www.youtube.com/watch?v=Bu52Q2HAVHs PARTE 1

https://www.youtube.com/watch?v=R3yaqajgnyQ PARTE2

domingo, 19 de enero de 2014

PHI

El número áureo o de oro representado por la letra griega φ es un número irracional.

Se trata de un número algebraico irracional (su representación decimal no tiene período) que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción entre dos segmentos de una recta. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza: en las nervaduras de las hojas de algunos árboles, en el grosor de las ramas, en el caparazón de un caracol, en los flósculos de los girasoles, etc.

Asimismo, se atribuye un carácter estético a los objetos cuyas medidas guardan la proporción áurea. Algunos incluso creen que posee una importancia mística. A lo largo de la historia, se ha atribuido su inclusión en el diseño de diversas obras de arquitectura y otras artes, aunque algunos de estos casos han sido cuestionados por los estudiosos de las matemáticas y el arte.

El número áureo surge de la división en dos de un segmento guardando las siguientes proporciones: La longitud total a+b es al segmento más largo a, como a es al segmento más corto b.

Cálculo del valor del número áureo

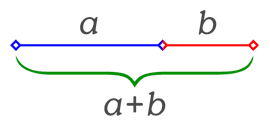
Dos números a y b están en proporción áurea si se cumple:

$\frac{a+b}{a}=\frac ab$

Si $\varphi$ es igual a $\frac ab$ entonces la ecuación queda:

$1 + \varphi^{-1} = \varphi$

Multiplicando ambos miembros por $\varphi$ , obtenemos:

$\varphi + 1 = \varphi^2$

Igualamos a cero:

$\varphi^2 - \varphi - 1 = 0$

La solución positiva de la ecuación de segundo grado es:

$\frac{1+\sqrt{5}}{2}=1\textrm{.}61803398874989\ldots$

que es el valor del número áureo, equivalente a la relación $\frac ab$ .

Hay una relación especial entre la razón aúrea y los números de Fibonacci (0, 1, 1, 2, 3, 5, 8, 13, 21, ... etc, cada número es la suma de los dos números delante de él).

Que a la ves evoluciona sustituyéndose para dar a phi como valor.

Si tomas dos números de Fibonacci consecutivos (uno detrás del otro), su cociente está muy cerca de la razón de oro:

A	B	B / A
2	3	1,5
3	5	1,666666666...
5	8	1,6
8	13	1,625
13	21	1,615384615...
...	...	...
144	233	1,618055556...
233	377	1,618025751...
...	...	...

http://www.disfrutalasmatematicas.com/numeros/naturaleza-razon-oro-fibonacci.html

https://www.youtube.com/watch?v=j9e0auhmxnc

PI

π (pi) es la relación entre la longitud de una circunferencia y su diámetro. Es un número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería. El valor numérico de π, truncado a sus primeras cifras, es el siguiente:

$\pi \approx 3,14159265358979323846 \; \dots$

La necesidad de calcular la longitud de una circunferencia conociendo su diámetro fue común en varias civilizaciones antiguas, por lo cual no es de sorprender que

desde desde tiempos antiguos ya existan referencias al valor de π, si bien no se le conocía con ése símbolo ni su valor exacto.

1650 AC: En el Papiro Rhind, el escriba Ahmes calcula el área de un círculo de diámetro 9 usando π = 3,1405.

Antigua papiro egipcio de Rhind

El matemático griego Arquímedes (siglo III a. C.) fue capaz de determinar el valor de π entre el intervalo comprendido por 3 10/71, como valor mínimo, y 3 1/7, como valor máximo. Con esta aproximación de Arquímedes se obtiene un valor con un error que oscila entre 0,024% y 0,040% sobre el valor real. El método usado por Arquímedes era muy simple y consistía en circunscribir e inscribir polígonos regulares de n-lados en circunferencias y calcular el perímetro de dichos polígonos. Arquímedes empezó con hexágonos circunscritos e inscritos, y fue doblando el número de lados hasta llegar a polígonos de 96 lados.

Alrededor del año 20 d. C., el arquitecto e ingeniero romano Vitruvio calcula π como el valor fraccionario 25/8 midiendo la distancia recorrida en una revolución por una rueda de diámetro conocido.

En el siglo II, Claudio Ptolomeo proporciona un valor fraccionario por aproximaciones:

$\pi \simeq \frac{377}{120} = 3{,}1416 \ldots$

En la imagen se observa como una rueda de diámetro 1 gira y va dejando su huella. Donde termina la huella es la longitud de la circunferencia en relación al diámetro, en otras palabras, Pi.

https://www.youtube.com/watch?v=G-O2Afx9DjA

--ZONA PRO-- (NO NOOBS ALLOWED)

Esta sección no es para noobs de 4to de prepa, pensándolo bien, ni para los de 5to de prepa, quizá apenas para los muy inteligentes de 6to de área 1. La única apta para esta sección es la Maestra y con mucho esfuerzo, el dueño de la CANACA.

Todo eso es para que se de una idea de la complejidad de este tema y lean otra sección ultra-simplificada para su estudio.
(Esta sección solo existe para mostrar a la Maestra el trabajo bueno para la calificación)

El número Pi tiene muchísimas ecuaciones para su cálculo, sin embargo, no todas son exactas, ya que provienen desde la antiguedad. He aqui las mas efectivas:

La primera es la formula de Euler, la segunda es la función de Euler con la zeta de Riemann
la tercera es la suma de Leibniz y la cuarta es el producto de Wallis.

Sin embargo, la más efectiva y la cual es usada actualmente por computadoras chimba es:

Aunque esta toda grande y fea, es efectiva y se calculan muchos valores exactos de Pi.
http://mimosa.pntic.mec.es/jgomez53/matema/conocer/pi_10000.htm

El número e tambien tiene sus fórmulas profesionales, sin embargo solo voy a mencionar las autenticas primeras, osea, la del mismo Euler:

QUE ES IGUAL:

Actualmente es reconocido con la serie de Taylor o Mclaurin con:

El número Phi, me da flojera poner todo ya que también es muy poderoso, es más poderoso que los demás. Lo único que les puedo decir es que esta TODOS lados. Cheque la sección de Phi para ver su ecuaciones simples que lo pueden aproximar.