El Lado Oculto de los Irracionales: PHI

El número áureo o de oro representado por la letra griega φ es un número irracional.

Se trata de un número algebraico irracional (su representación decimal no tiene período) que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción entre dos segmentos de una recta. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza: en las nervaduras de las hojas de algunos árboles, en el grosor de las ramas, en el caparazón de un caracol, en los flósculos de los girasoles, etc.

Asimismo, se atribuye un carácter estético a los objetos cuyas medidas guardan la proporción áurea. Algunos incluso creen que posee una importancia mística. A lo largo de la historia, se ha atribuido su inclusión en el diseño de diversas obras de arquitectura y otras artes, aunque algunos de estos casos han sido cuestionados por los estudiosos de las matemáticas y el arte.

El número áureo surge de la división en dos de un segmento guardando las siguientes proporciones: La longitud total a+b es al segmento más largo a, como a es al segmento más corto b.

Cálculo del valor del número áureo

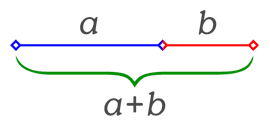
Dos números a y b están en proporción áurea si se cumple:

$\frac{a+b}{a}=\frac ab$

Si $\varphi$ es igual a $\frac ab$ entonces la ecuación queda:

$1 + \varphi^{-1} = \varphi$

Multiplicando ambos miembros por $\varphi$ , obtenemos:

$\varphi + 1 = \varphi^2$

Igualamos a cero:

$\varphi^2 - \varphi - 1 = 0$

La solución positiva de la ecuación de segundo grado es:

$\frac{1+\sqrt{5}}{2}=1\textrm{.}61803398874989\ldots$

que es el valor del número áureo, equivalente a la relación $\frac ab$ .

Hay una relación especial entre la razón aúrea y los números de Fibonacci (0, 1, 1, 2, 3, 5, 8, 13, 21, ... etc, cada número es la suma de los dos números delante de él).